Dot ProductIf you can add two vectors, you might then ask if you can multiply two vectors. Vectors can be multiplied in two different ways, each of which has a slightly different interpretation.
As vectors indicate quantities with direction, vector multiplication also depends on direction. Sometimes we are interested in events for which if two vectors are parallel, we get a large effect, but if they are perpindicular, they have very little effect. To be more rigorous, the dot product represents multiplying one vector with the component of a second vector onto the first. If two vectors are at right angles, the dot product is zero. If they are parallel, the dot prduct is just the product of the magnitudes. 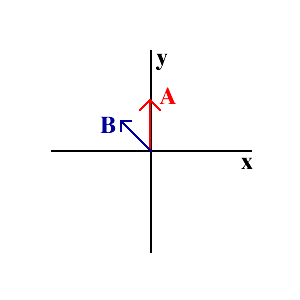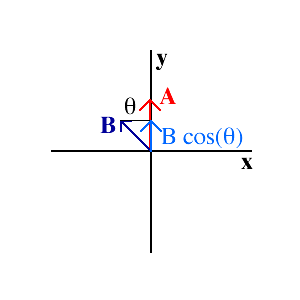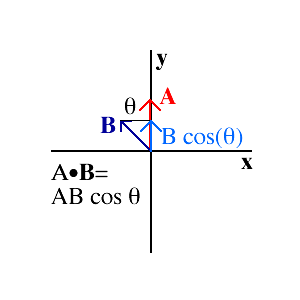 Note that the dot product produces a scalar result.
Suppose you are blowing bubbles, and you want to know how much flux would go through a bubble ring. The area of the ring in this case could be considered a vector, where surfaces areas are generally written as a vector with a direction which indicates which way the area is facing. This is often referred to as the direction "normal" to the surface. For example, if the broad part of the bubble ring is facing you, it's area vector is pointing towards you. The following image shows the direction of the surface area of the opening of a bubble ring, relative to the buble ring. The image is rotating counter clockwise about the y axis, so the left side of the image is coming towards you, and the right side is moving away from you.  The dot product, sometimes called the inner product, can be used for this. The dot product of A and B is written as A.B and spoken as "A dot B". A.B=A B cos This can also be written in terms of coordinates, where the dot product is the sum of the product of each vectors components. In three dimensions this would be A.B=AxBx +A yBy + AzBz. The flux of air rushing through the center of the bubble ring is given by v.A. If the ring is facing in the same direction as the wind, you get the most wind through the ring. Report technical/content problems here |