Dialysis Two Compartment Model

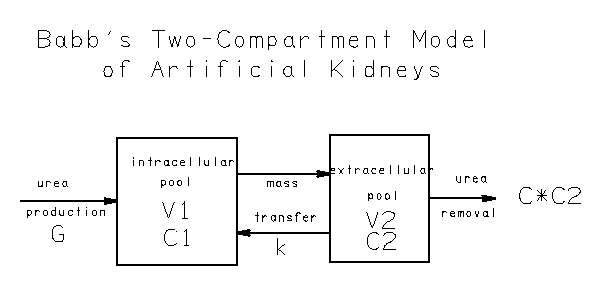
The mathematical model to describe dialysis treatment is based on a two compartmental model similar to Babb's 1967 model (Cooney, 335). Although this model depicts only urea dynamics, it could be altered to model other blood solutes. Urea works particularly well for this model because of its high permeability in aqueous environments. Its permeability allows it to move freely between the compartments. More importantly, urea concentration is the most widely used measure of dialysis effectiveness (Depner, 6).

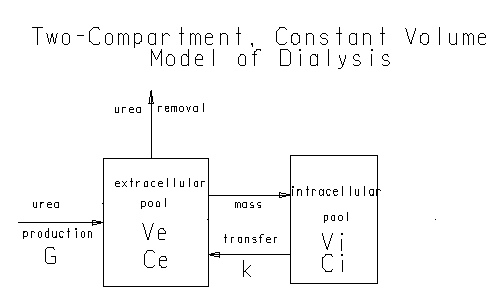
The model depicted above was altered slightly to account for research since 1967. Recently, research indicates that urea generation occurs mostly extracellularly, so the model was revised to reflect the urea movement into the extracellular pool rather than the intracellular pool. The intracellular urea flux is generated by a concentration gradient at the cell wall. The gradient creates urea movement between the intracellular and extracellular compartments. For ease of calculation, the volumes in the two compartments are assumed to be constant in this model. The total body water volume is computed as sixty percent of body weight. The intracellular volume is 2/3 of the total volume, while the remaining 1/3 is the extracellular volume. The mass transfer coefficient used in the calculations is 800 ml/min. This value for urea is an average across all body tissues that was determined in clinical studies. Depending on the percent of renal failure, the urea removal is a combination of the dialyzer and residual kidney function.

The equations used to generate the computational model are as follows:

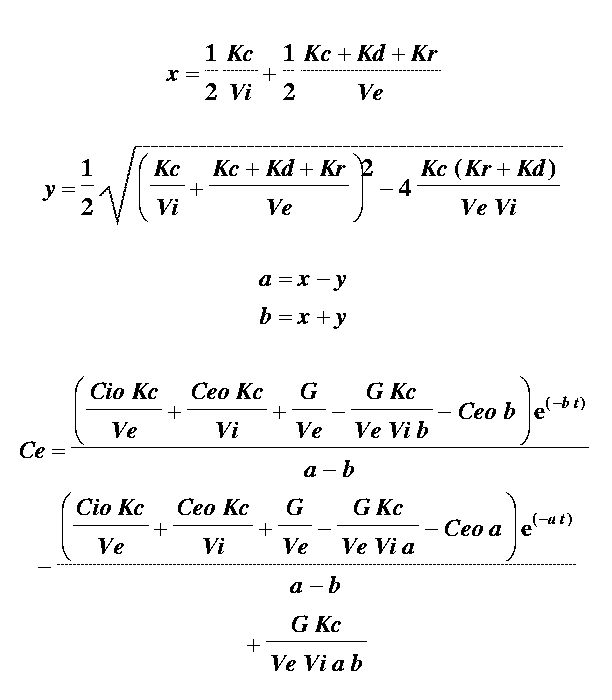
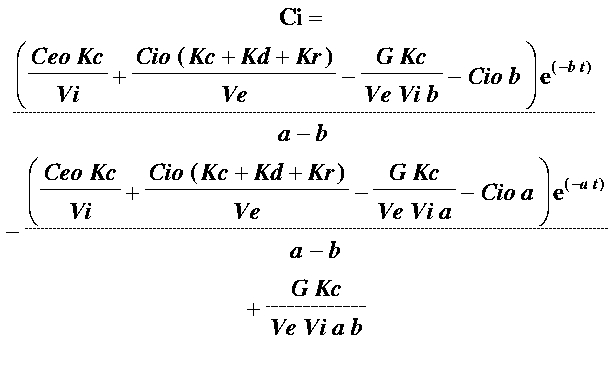
where,

Kc = urea transfer coefficient (ml/min)
Kd = dialyzer clearance (ml/min)
Kr = kidney clearance (ml/min)
Ve = extracellular compartment volume (ml)
Vi = intracellular compartment volume (ml)
Ce = extracellular urea concentration (mg/ml)
Ci = intracellular urea concentration (mg/ml)
Ceo = Ce at time zero - same as Predialysis BUN Value*100
Cio = Ci at time zero - same as Predialysis BUN Value*100
G = urea generation rate (mg/min)
t = time (min)

Currently, resesearch in dialysis modeling is moving away from the two compartment model. The new emphasis is on developing models that more closely resemble the physiology of the body. For the purpose of teaching about dialysis, the two compartment model is adequate. If you are interested in more advanced models, Dr. John T. Daugirdas, M.D. of the University of Illinois at Chicago et al has developed a multicompartmental "Regional Blood Flow Model" based on urea transport through the body. His May 1997 lecture is available via the HDCN Electronic Journal.