Mentor: If I have two sets of numbers, is it possible for the sets to have elements in common? Can an element be in both sets?

Student 1: Well... 5 is an odd number, and it's also a prime number....

Mentor: Great! So, elements can be part of two sets at once. I'm going to draw a picture to represent that, and you all can help me put some elements in the correct place.

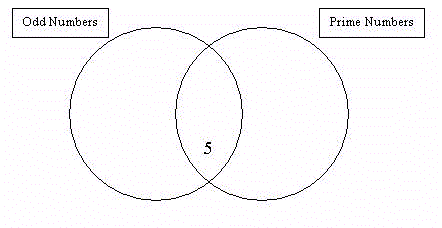Student 2: Well, it's a prime number and an odd number, so the way you drew it, it's clear that it is a part of both circles!

Mentor: So what should we call those circles?

Student 2: They are sets, aren't they?

Mentor: Wonderful! Can anyone think of another number that I could put in this diagram? What about a number that is odd, but that isn't prime?

Student 3: You could put the number nine in the odd number circle, but not in the prime number circle, because it's divisible by 3.

Mentor: Perfect answer! What we are making here is called a Venn Diagram. Sometimes they have two circles, like the one we have drawn here, and sometimes they have more! Let's put a few more elements in this one, then we can try to create a Venn diagram with three circles...

Continue to allow students to suggest elements until you feel they understand Venn diagrams.