Student: In the Tessellation activity, the same shape is repeated over and over to make the pattern. Isn't this a type of symmetry?

Mentor: Yes. There are many symmetries in tessellations. However, you need to be careful that you don't confuse line symmetry with the type of symmetries that we find in the plane of a tessellation. Can you tell me what you mean by symmetric?

Student:: I think a figure is symmetric when a line can divide the figure into two congruent halves. A butterfly is an example. If I draw a line down the center of the butteryfly's body, each half of the butterfly looks the same, like a mirror r eflection.

Mentor: That's right. What you are describing is called line symmetry, though line symmetry is only one of several types of symmetry. A more precise definition of line symmetry is that if you draw the line of symmetry, each point on one side of the line has a corresponding point on the opposite side of the line. If you connect these two points, that line is perpendicular to the line of symmetry.

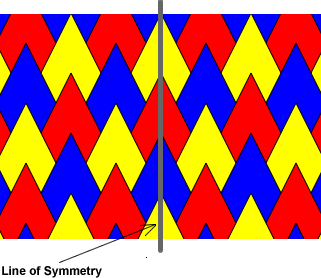When we are talking about an infinite plane, we refer to the symmetries we find as plane symmetries or geometric transformations.

Student: Well, I guess by my earlier definition, no because there is nowhere I could draw a line and have the pattern reflect on itself. But you mentioned something about there being other types of symmetries than just line symmetry so now I'm thi nking that the answer is actually yes.

Mentor: Your intuition is correct. There are three other types of symmetry in a plane. They all move a pattern in a way that the pattern still matches the original pattern exactly. What other movement can we make to this pattern so that the pattern's appearance doesn't change?

Student:We could slide the whole pattern sideways.

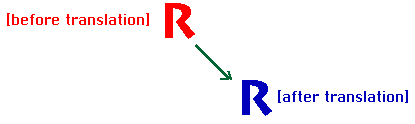
Mentor: Correct! This kind of symmetry is called a translation. All translations have a direction and a distance. Can you make a tessellation that does not have translational symmetry?

Student: Part of the definition of a tessellation is that it is a repeating pattern. So, I think all tessellations have translational symmetry!

Mentor: Good observation. In what other way can you transform the pattern?

Student: I could spin the pattern around a point, rotating it. That would leave the pattern unchanged.

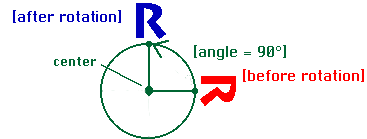
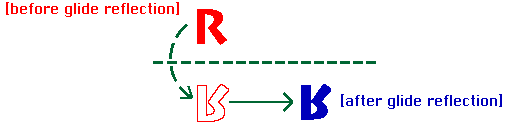
Mentor: This is called rotational symmetry. Rotations always have a center, and an angle of rotation. Can you find one more way to transform the tessellation?

Student: The only other thing I could do to the pattern would be to reflect it across a mirror line and then translate the pattern. But does that count? I am combining two types of symmetry.

Mentor: Actually, that is indeed the last type of symmetry and it is called glide reflection. This is the only type of symmetry that involves two steps: a reflection with a translation along the mirror line. Glide reflections are a separate type of transformation because some tessellations have glide reflections, but not reflections or translations.

Now, see if you can make tessellations with different combinations of transformations.