Interactivate

Patterns in Pascal's Triangle
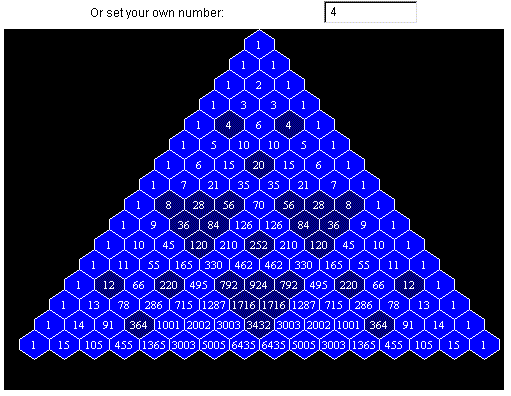
Shodor > Interactivate > Lessons > Patterns in Pascal's Triangle

Abstract

This lesson is designed to show students that patterns exist in the Pascal's Triangle, and to reinforce student's ability to identify patterns.

This is a good follow up lesson to Patterns in Fractals.

Objectives

Upon completion of this lesson, students will:

  • have been introduced to Pascal's Triangle and its patterns
  • have practiced identifying and determining patterns in Pascal's Triangle .

Standards Addressed:

Textbooks Aligned:

Student Prerequisites

  • Arithmetic: Student must be able to:
    • perform integer and fractional arithmetic
  • Technological: Students must be able to:
    • perform basic mouse manipulations such as point, click and drag
    • use a browser for experimenting with the activities.

Teacher Preparation

Key Terms

combinatoricsThe science that studies the numbers of different combinations, which are groupings of numbers. Combinatorics is often part of the study of probability and statistics
fractalTerm coined by Benoit Mandelbrot in 1975, referring to objects built using recursion, where some aspect of the limiting object is infinite and another is finite, and where at any iteration, some piece of the object is a scaled down version of the previous iteration
multiplesThe product of multiplying a number by a whole number. For example, multiples of 5 are 10, 15, 20, or any number that can be evenly divided by 5

Lesson Outline

  1. Focus and Review

    Remind students what has been learned in previous lessons that will be pertinent to this lesson and/or have them begin to think about the words and ideas of this lesson.

    • Ask the students to recall what a multiple is and to think of an example. Have a student share his example with the class
    • Have the students also consider Pascal's Triangle. If your class has not studied it previously, ask students, "Did you know that multiples make a pattern in Pascal's Triangle?"

  2. Objectives

    Let the students know what it is they will be doing and learning today. Say something like this:

    • Today, class, we will be talking about the patterns that multiples create in Pascal's Triangle
    • We are going to use the computers to learn about these patterns, but please do not turn your computers on or go to this page until I ask you to. I want to show you a little about Pascal's Triangle and its patterns first.

  3. Teacher Input

    In this part of the lesson you will explain to the students how to do the assignment. You should model or demonstrate it for the students, especially if they are not familiar with how to use our computer applets.

    • You may need to lead a discussion on Pascal's Triangle
    • Check to be sure that the students understand how to make Pascal's Triangle by having them create a portion on paper, or by drawing one on the board or overhead projector as they tell you what to write.
    • Open your browser (but don't let the students open theirs yet) to Coloring Multiples in Pascal's Triangle in order to demonstrate this activity to the students. Ask students if the triangle that they created looks like the one displayed on the screen.
    • You must now explain the applet to the students. This can best be done by setting your own number: 4 is a good number to choose when explaining this to students
    • Ask students to name multiples of 4 that they see in the triangle. They will probably name numbers such as 4, 8, 12, 20, 28, and 36. Click on these numbers to highlight them as the students call them out
    • You may have to give hints to help students determine the larger multiples of: 56, 84, 120, 220, 252, 364, 792, 924, 1716, and 3432. Encourage the students to look for the pattern and make an educated guess about the larger multiples of 4.
    • Ask a student to describe the pattern that she sees after all the multiples have been found. Ask the students what types of shapes are made by the multiples within the Pascal's Triangle.
    • Pass out the Worksheet to Accompany "Finding Patterns in Pascal's Triangle." Have the students draw the pattern that the class determined as a group for multiples of 4 in Pascal's Triangle.

  4. Guided Practice

    Try another example, letting the students direct your moves. Or, you may simply ask, "Can anyone describe the steps you will take for this assignment?

    • If your class seems to understand the process for doing this assignment, simply ask, "Can anyone tell me what I need to do to complete this worksheet?" or ask, "How do I run this applet?"
    • If your class seems to be having a little trouble with this process, do another example together, but let the students direct your actions:
      • This time, choose a number such as 8 to try the example with. Let the students call out multiples of 8 that they see in the triangle."
      • The multiples of 8 include: 8, 56, 120, 792, and 3432. You might want to ask students to compare this pattern to the one that was formed by the multiples of 4. Be sure to point out that all of the multiples of 8 are also multiples of 4 and yet the patterns are very different (since the multiples of 4 are not necessarily multiples of 8)

  5. Independent Practice

    • Allow the students to work on their own to complete the rest of the worksheet. Monitor the room for questions and to be sure that the students are on the correct web site.
    • Students may need help with finding the multiple of the harder numbers, such as 7. Encourage the students to devise their own methods for determining the multiples. Suggest that the students attempt to use their knowledge of the patterns they already discovered to aid in finding the harder patterns!

  6. Closure

    It is important to verify that all of the students made progress toward understanding the concepts presented in this lesson. You may do this in one of several ways:

    • Take up the individual or group worksheets to evaluate for completion
    • Bring the class together and have different groups or individuals share their result for a particular number with the rest of the class. Allow students who did not get to finish that number to sketch the result so that they will not lack some of the information needed for full understanding
    • Have the students write a short paragraph explaining the type of patterns that they saw including the similarities between the different pictures, and the type of shapes that recurred in the pictures

Alternate Outline

This lesson can be rearranged in several ways:

  • The students may wish to tackle the worksheet in groups.
  • You may wish to assign different groups with particular numbers to ensure that every option is attempted for the class discussion later.

Suggested Follow-Up

  • As an extension, you may have students predict the entended pattern for a particular number when the Pascal's Triangle is made larger. The class could work together to extend the triangle by hand (on a bulletin board, perhaps) and see if the predictions were correct. Again, 4 may be a good number to use for this extension.

  • You may wish to do a similar lesson to discuss patterns formed by Coloring Remainders in Pascal's Triangle This activity may prove to be a little more challening for students, may require more supervision, and may best be done as a class discussion and demonstration.

a resource from CSERD, a pathway portal of NSDL NSDL CSERD