An Introduction To Quadrilaterals
AbstractThis lesson is designed to introduce students to quadrilaterals. Included in this lesson are discussions of parallelograms, rectangles, and trapezoids. ObjectivesUpon completion of this lesson, students will:
Standards Addressed:Textbooks Aligned:Student Prerequisites
Teacher Preparation
Key Terms
Lesson Outline
Alternate OutlineGroups of students may take turns creating a quadrilateral and proving that it has the characteristics necessary to define that shape.
Suggested Follow-Up
|

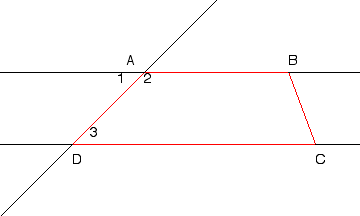 Remind them that angles 1 and 3 are congruent (since alternate interior angles are
congruent), and angles 1 and 2 are supplementary (since the two angles form a linear
pair), therefore angles 2 and 3 should be supplementary, if the lines are parallel.
Remind them that angles 1 and 3 are congruent (since alternate interior angles are
congruent), and angles 1 and 2 are supplementary (since the two angles form a linear
pair), therefore angles 2 and 3 should be supplementary, if the lines are parallel.