Translations, Reflections, and Rotations
|
Mentor: We all know that we see our "reflection" in a mirror. If I draw a triangle on the board and this "mirror," what would the reflection look like? 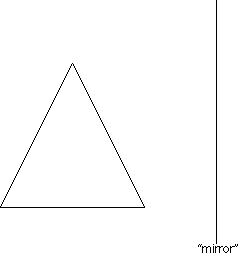
Student 1: Well, I think that it would look just the same on the other side of the line. Like this: 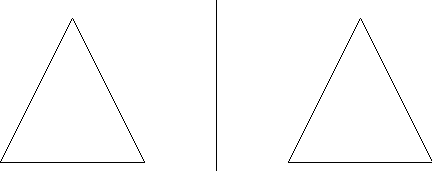
Mentor: If I make an "X" on this line on the original triangle, where would it be on the reflected triangle? 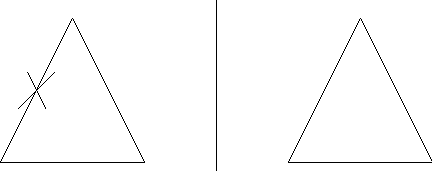
Student 2: Well, when we reflected the triangle, we sort of flipped it over that "mirror," or the line, so it would be on the opposite side of the triangle, like this: 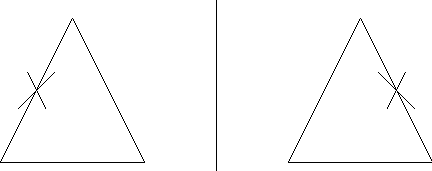
Mentor: Great! We call that line the line of symmetry. See, the picture is symmetrical in respect to the line. Now that we know what it means to reflect an object, what do you think it means to rotate an object? Student 3: I think it means that we just turn it. Kind of like putting the object on a plate, and then spinning the plate around while the plate's center stays in one place. Mentor: That's good. The center of the object doesn't have to be at the center of rotation i.e. The center of your plate. Any point can be used to mark the center of rotation. Do you see I've put an "x" on one of the vertices of the triangle? Can you draw what this triangle would look like if we rotated it 90 degrees around this vertex? Student 3: I think it would look like this: 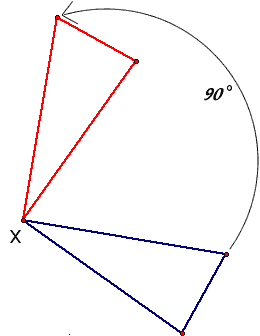
Mentor: Very nice. And also, it is customary that the angle of rotation is measured in a counterclockwise direction, just like you drew it. Now we have one more transformation that we can do. Who can guess what it means to translate an object? Student 4: Is that like moving it over? Mentor: Good! A translation is like sliding the object over a certain distance. If I translated this triangle about 14 cm, who could draw what it would look like? Student 4: I think it would look like this: 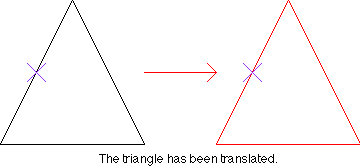
Mentor: Very nicely done! Thank you for including the "x" on the appropriate side of the triangle. |
