Tables and Combinatorics
|
Mentor: A player wins if one of his numbers comes up as the sum of two dice. Player 1 wins if the sum is 4, Player 2 wins if the sum is 5, and player 3 wins if the sum is 6. Is the game fair? Student 1: It is fair, because each player has one winning number. Student 2: Wait a minute! There are many ways for each sum to show on the dice. For example, the sum of 4 can appear in three ways:
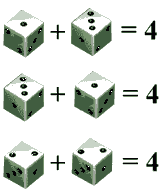
Student 3: We have to count all the cases somehow.
Mentor: Right, we do not want to miss any outcomes. Let us make a list of all of them. The first number we write will stand for the first die and the second number will represent the second die. It is faster to write only numbers without drawing the dice, of course. We will write all the pairs that start with 1 first, then all the pairs that start with 2, and so on. 1-1 1-2 1-3 1-4 1-5 1-6 2-1 2-2 2-3 2-4 2-5 2-6 3-1 3-2 3-3 3-4 3-5 3-6 4-1 4-2 4-3 4-4 4-5 4-6 5-1 5-2 5-3 5-4 5-5 5-6 6-1 6-2 6-3 6-4 6-5 6-6 Mentor: Now we have all the outcomes listed. Does it help us to decide which player has better chances of winning? Student 1: Not much. We have to go through the whole list looking for pairs that add up to the winning numbers. It was so boring to write all the numbers like that! Student 2: I just noticed that there are two errors in the list. Mentor: Oops. I guess this way is not very reliable and not much fun. We can exploit the structure of the problem by transforming the list into more elegant, economical and clear form: a table.
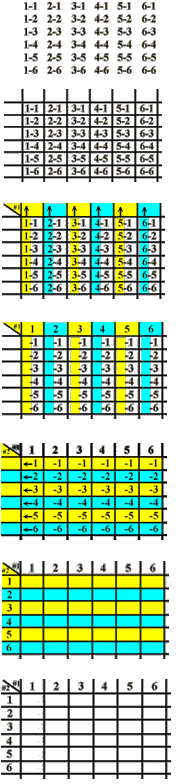
Mentor: Figuring out how to transform data lists into a table or tree should only be difficult on your first couple of tries. When you know how to do it, then you can proceed directly to the last step. We can put any additional information that we want into the empty table. Right now, we need the sums of the numbers on the dice to determine which player wins. Can you put the sums into the table? Student: My pleasure:
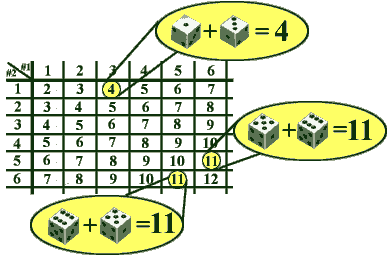
Mentor: Now it is easy to answer questions about the game. Is it fair? Student: Nope. Player 1 has 3 winning outcomes, Player 2 has 4 winning outcomes, and Player 3 has 5 winning outcomes out of 36. Player 3 will win more often if they play for a long time. Mentor: How did you get 36? Student: Well, we have a table six by six, so there are 6*6=36 different outcomes for the game. Mentor: The science that studies the numbers of different combinations is called combinatorics (big surprise!) There are many beautiful, interesting problems in combinatorics. We will come across some of them in these probability units. How many different outcomes would there be if we had two coins instead? Student: Let us see. Now there are two possibilities for the first coin, heads and tails, and two possibilities for the second coin. That makes 2*2=4 outcomes. We can put the outcomes in a table 2 by 2. Mentor: What if we had a coin and a six-sided die? (12) If we had a ten-sided and an eight-sided dice? (80) If we had two spinners with numbers from 1 to N and from 1 to M? (N*M) You may have already noticed the rule: we multiply! This is a very famous rule: If you can choose two things, and there are M choices for the first and N choices for the second, you can have M*N different combinations. Mentor: Can you find some examples of this rule in work? Student 1: Say, if you want to choose between a sports car, a van, and a truck, and they can be of four colors, then you'll have 12 possible combinations.
Student 2: A table can be used here, too. Even little children would understand it:
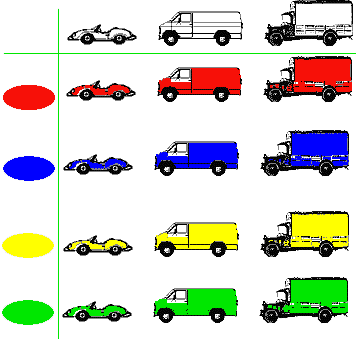
Student 3: We use the same thing to write multiplication table. Here is the table up to 6:
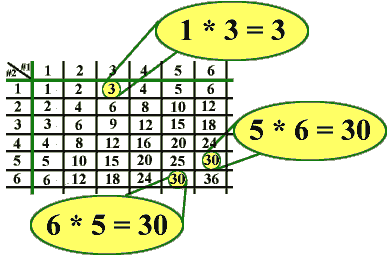
|
