Standard Deviation
|
Student: Can you explain what standard deviation means? I'm doing a project in my biology class and we have to use it, and I don't understand it. Mentor: Sure. Let me think of an example that you would be familiar with...hey, your brother is a sharpshooter for the Marines, isn't he? Student: Yeah. Mentor: Okay, what do you think a really good sharpshooter's target would look like? Would they get all the bullets to go into exactly the same hole? Student: Well, no sharpshooter is perfect--you can't hold a rifle perfectly still. It's going to move at least slightly. So their shots would be close together, but not in the same spot. Mentor: Exactly. There is going to be a little bit of what we call "random variation". One time it might be a little up and to the left, the next time just slightly right, and so on. You cannot predict the next variation, but if you look at all of the variations together you can get an idea of how skilled the shooter is with a rifle by seeing if the variation is large or small. Student: Ok, I see. Mentor: Good. Now, we can link this back to your original question. Standard deviation is the name for one way of looking at how tightly (or loosely) grouped a set of data is. It lets you describe the variation in a whole set of data with a single number. This can be useful in finding out how similar all the parts of a group are. For instance, if you were producing items in a factory you could tell whether or not the people, or machines, producing your product are performing well, i.e. creating products with little variation. If the standard deviation began to increase, it may indicate that a machine part is wearing out. Student: Oh, that sounds useful. Now, about my biology project? Mentor: Yes, of course. Tell me what this project was about. Student: Well, I planted a bunch of beans, and grew one set under incandescent light and one set under fluorescent light. And after three weeks I measured the lengths of all the stalks, and I'm supposed to compute the mean length and the standard deviation of each group. I know how to get the mean, just add all the lengths and then divide by the number of stalks, but I didn't understand the formula for getting the standard deviation.
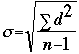
Mentor: It does look scary, but really it is just several easy steps squished into one expression. So, as with most complex mathematical expressions, the best way to tackle this one is from the inside out. Let's start with that funky zigzag-looking thing. Student: My teacher told us that is was a Greek letter, sigma, I think. Mentor: Yes, it is. It is the Greek letter for " S", and we use it to mean "sum", or "add up". It is telling you to add up each of the d squareds. Student: What are the d squareds? Mentor: For each number in your data set, d is the difference between that number and the mean. And d squared is just d times itself. So you simply take each number, subtract it from the mean, and square your result, then add them all up. Students: So that takes care of the sigma. Is the next step to divide by n-1? Mentor: Exactly, divide the sum of the d squareds by n-1, where n is the number of data points. Now, once you have completed that, what does the big bracket tell you to do? Student: Take the square root? Mentor: Right! That's all there is to it. So what's your result? |
