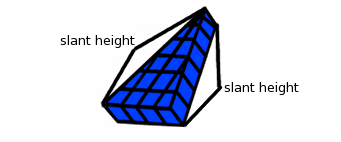
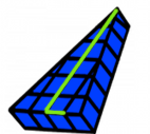
Slant Height
|
Student: What is the slant height of a triangular prism? Mentor: Let's start with looking at the triangle portion of a triangular prism.
Mentor: The four cubic units on the wide part of the triangle represent the base width of the triangle. The distance from the middle of the base width to the top peak of the triangle is the base depth. The actual lengths of the triangle's edges that run from the base to the top peak of the triangle represent the slant height.
Student: OK, so the slant height is 6 units, right? Mentor: Actually, no. The slant height is going to be a bit more than the base depth because the distance from the corner of the base edge to the top peak (representing slant height) is greater than the distance from the center of the base edge straight up to the top peak (representing base depth). Student: I can see how that would be longer, how much longer is it? Mentor: Well, let's try to figure out what the slant height would be for this triangular prism and we can see for ourselves. How are we going to find the measurement of one of the diagonal sides of the triangle representing the slant height? Student: Well, we could use the Pythagorean theorem! We know the base depth of the triangle (6), which will be one leg of the triangle. That line will bisect the base width and create a right triangle. Mentor: Right! Since we are bisecting the base width what will the part that forms a right triangle measure? Student: Bisect means to divide into two equal parts so the base width (4) divided by 2 would be two. Mentor: So the triangle that we created within this triangle has one leg that measures 6 (the base depth) one leg that measures 2 (half of the base width) and the diagonal, which represents the slant height of the triangle. What next?
Student: Well, now I can apply Pythagorean theorem. The Pythagorean theorem is: a 2 + b 2 = c 2 Mentor: Which variable represents the slant height? Student: The slant height is c because the hypoteneuse of a right triangle is always represented by the variable c while the two legs that form the right angle are variables a and b. Mentor: You really know how to use this equation! What do you do next? Student: I plug in the values. One leg was 2 units and the other leg was 6 units so: (2) 2 + (6) 2 = (c) 2 4 + 36 = c 2 40 = c 2 c= √40 So c is about 6.32 units Mentor: Wow you just found the slant height! Great work. Student: So the slant height for this example would be 6.32 because that is the length of each edge that runs from the base of the shape to the top peak! |