Probability and Geometry (elementary)
|
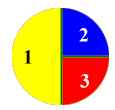
Mentor: In the game we will study, players make a spinner, then agree on what each of them wins if his or her color is chosen. For example:
Player 1 wins 10 points when the spinner stops at yellow. Player 2 wins 10 points when the spinner stops at blue. Player 3 wins 10 points when the spinner stops at red. Is the game fair? How can you tell? Student: No, it's not fair. Player 1 will win more points. Mentor: How do you know. It's just chance. Student: Because the yellow part is bigger. The spinner is going to land there more often. Mentor: Why do you think that is? Student: The spinner can land anywhere in the circle, but half the circle is yellow. Half the time, the spinner is going to land in the yellow. Mentor: You're right, the spinner has a 1 in 2 (or 1/2) chance that it will land in the yellow section. What fraction tells you how likely it is that the spinner will land in the blue or red? Student: If the yellow is 1/2, then the blue is 1/4 and so is the red. So they each have a 1/4 chance that the spinner will land in their section.
Mentor: Right! You're saying that whatever fraction of the spinner a certain color is, that's how
likely it is that the spinner will land in it's section. It's easy to see in a spinner like
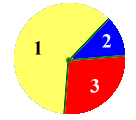
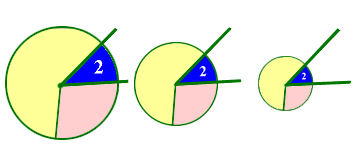
that first one. But imagine a spinner like this:
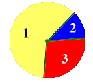
How do we measure each player's chances now? Student: It would be nice if we could measure each player's "slice" exactly. How would you do it? Mentor: People measure things by comparing them with standard units. You can say that a show is 25 minutes long, a tree is 12 meters high, or a dog weighs 23 kilograms. We can use certain units to measure each player's "slice," or sector, of the spinner. Before we start, please tell me what is different and what is the same about these three spinners:
Student: It does not matter for the game which of the spinners is used. The chances of each color being chosen are the same. Mentor: Why do you think that is? Student: The angles of each color are the same.
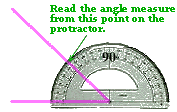
Mentor: Traditionally, people measure angles in special units called " degrees." These units were chosen in such a way that the following easy-to-measure angle is 90 degrees:
This angle is called a right angle. A third of the right angle is 30 degrees, for example, and so on. There is a useful tool that can be used to measure angles. It is called a protractor . It has units for degrees, much like a ruler has units for centimeters or inches. You can measure an angle by aligning the bottom of the protractor with one side of the angle, placing it so that the center of the protractor is at the vertex of the angle:
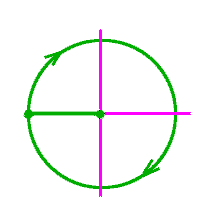
Student 1: The whole circle's angle is 360 degrees, because there are four right angles in it:
It means that each player has as many chances as his angle has degrees, out of the total of 360 chances. Mentor: What angle will give you a 1/3 probability of winning? Student: A third of 360 degrees, or 120 degrees. Mentor: You can make some spinners for the game and find the exact chances of each player winning by measuring angles. Make the game fair by choosing how many points each player wins. Then play the game many times and see if the chances and actual winnings are close to what you predicted. |