Probability and Outcome
|
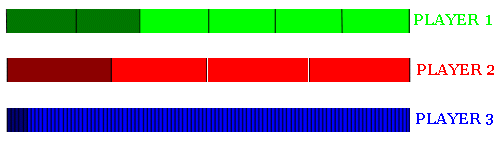
Mentor: Let us look at several people playing simple chance games. Player 1 rolls a six-sided die and wins if it shows numbers 2 or 3, losing otherwise. Player 2 rolls a four-sided die and wins if it shows a 1. What are the chances of each player winning? Student: We can say that the first player wins in two out of six possible cases. Mentor: Scientists also use the word outcome instead of the word "case." Each outcome is a complete description of a situation that can happen as a result of an experiment (just the important information). In our game, the number that shows up on the die is all that interests us: we do not care how long the die rolls, how far from each player it falls, and so on. Which player has a better chance of winning and why? Student: Player 1 will win more often, because he wins in two cases and Player 2 only in one case. Mentor: Is it so? Let me introduce Player 3 who uses a big spinner with numbers from 1 to 100. Player 3 wins if the spinner stops at 96, 97, 98, 99 or 100. Out of three players, who wins more often and why? Student: Now Player 3 wins in five cases. This is more than the other two players have, but there are a hundred cases there.... Just counting cases is not enough! Mentor: Let us think about a different problem for a while. It will help you see some things. Suppose we have three players again, only now they play a different game. Each of them has a long rectangular box having the same length and width, a ball and a monkey. Each monkey throws a ball in each player's box in no particular manner, so it lands at a random spot inside the box. The bottoms of the boxes are divided into equal parts by thin lines. The parts are colored by light and dark colors, as shown on the picture. The box of Player 1 is divided into 6 parts, 2 of them dark; the box of Player 2 is divided into 4 parts, one of them dark; and the box of Player 3 is divided into 100 parts, five of them dark. If the ball lands in the dark part of the box, the player wins. Which player has better chances of winning?
Student: If the boxes are of the same length and width, then Player 1 has the most chances of winning, because his winning part is the largest. Mentor: What does this game have to do with the first game? Student: Player 1 wins in 2 out of 6 outcomes again, and Player 2 in 1 out of 4 outcomes. But in the second game each outcome of Player 1 looks smaller then each outcome of Player 2, and Player 3 outcomes are even smaller. They are tiny! In the first game, we do not know how "big" the outcomes are. Or do we? Mentor: This is a great question. Let us think about all possible outcomes for Player 1 in the first game, i.e., numbers 1,2,3,4,5 or 6 of the six-sided die. Now let us think about all the outcomes for Player 2, i.e., the numbers 1,2,3, or 4 of the four-sided die, and the outcomes for Player 3, i.e., all the numbers from 1 to 100 of the spinner. If each player were winning no matter what number showed on his die or spinner, he would win as often as every other player: always! This tells us that together all the possible outcomes of each player (e.g., numbers from 1 to 100 for Player 3) involve the same amount of "luck" as all the possible outcomes of any other player: all the luck one can have, 100% of luck and not some fraction of it. Student: So it makes sense to look at the "grand total" as a box that has the same length for each player, but a different number of "compartments"! It does not matter how the players choose the numbers, the meaning is the same. Now I can see how five winning outcomes for Player 3 mean much less chance than one winning outcome for Player 2! Mentor: We can draw pictures to compare chances. However, it is a tedious process. Pictures do not give us more information than numbers, they just help us to make sense out of the information. There are ways to make sense out of the numbers without pictures. To do that, we can express the chances, or the probability of each player winning, in different forms. Instead of saying: "The first player wins in two out of six outcomes," we can say: "The first player wins in two-sixth (or one-third, which is the same thing) of outcomes," or: "The probability of the first player winning is 1/3." And, of course, as 1/3=0.33 (rounded to two digits after the decimal point), we can say: "The probability of the first player winning is .33". If you look at the picture again, you can see that the dark area for Player 1 is indeed one third of the whole:
Student: Then the probability of Player 2 winning is .25. Mentor: There is yet another way of expressing probabilities. If something always happens, it means it happens in 100% of all cases. And if something happens half of the time, it happens in 1/2 of 100% of all cases, or 1/2*100%=50% of the cases. And if something happens in 1/3 of all the cases (that is the probability of Player 1 winning), we can say: "The probability of the first player winning is 1/3 of 100%, or 1/3 *100%=33.33%" rounded to two digits after the point." Student: So the probability of Player 3 winning is 5%. Mentor: Now let us do an experiment. Pretend you are Player 1. Play the game many times (100-200) using a die or a computer program and record the number of times you win (that is, the number of times you roll a 2 or 3). After each game, record the cumulative winning ratio, called experimental probability, in fractions and decimals. It is helpful to keep a chart that records the total number of games played and total number of games won. Experimental probability of winning=
Experimental probability of winning (in percents)=
Student: At first, the ratios change a lot with each new game. After many games they change less and less. I used a computer to simulate 1000 games, and the ratios stayed almost the same with each new game. They were close to .33 or 33%. Mentor: Why do you think experimental probability gets close to theoretical probability? |