Polar Coordinates
|
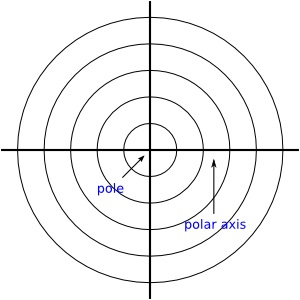
Mentor: You are probably familiar with the Cartesian coordinate system which allows you to plot points and functions on the coordinate plane. If you are given a set of points in the form (x, y), you should be able to plot them on the x- and y-axes of a graph. Student: Yes. If I were given the point (2,3), I would start at the origin and go two units to the right on the x-axis and then move up 3 units in the y direction. Mentor: That is correct. And if you were given a function, say y=2x+3, you could probably graph that too. Student: Of course, I would choose values of x which I would input into the function to get the values of y for that function. Then I would graph the points on the graph. Mentor: Yes! Did you know that you can also plot points on another type of graph based on the Polar Coordinate system. Student: What is the Polar Coordinate system? Mentor: The polar coordinate system is a circular rather than a rectangular coordinate system. You plot points given in terms of a value, r which is the distance from the center; and an angle measure which is given in degrees, or more usually radians. Do you remember what radians are? Student: Sure, they are another unit of measure for measuring angles. A circle contains 360 degrees which is the same as 2π radians. But, what would you use this system for? Mentor: Well sometimes it is more appropriate to describe a location in terms of a circular motion rather than a straight line. This system is well suited to trigonometric functions and is used in navigation because values can be plotted in terms of distance (r) and direction (angle, also referred to as the Greek letter theta shown as the symbol θ). Student: How would you plot points on a polar graph? Mentor: The polar coordinate system has axes similar to the Cartesian system and a point like the origin except that it is called the pole. It also has a ray that extends horizontally through the pole called the polar axis. Instead of a square grid, there are concentric circles centered at the pole that get uniformly bigger and radiate out from the pole. Polar coordinate plane looks like this:
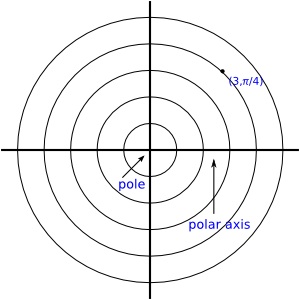
Mentor: Like rectangular coordinates, polar coordinates are also named with an ordered pair, but the meaning of each of the numbers is different. The first number in the coordinate pair, r, represents the distance from the pole and is like measuring the radius of a circle. The second number of the pair, θ, represents the angle measure, measured from the horizontal axis. The polar axis represents an angle measure of 0 radians or 0 degrees. Moving counterclockwise from this axis represents a positive angle measure and clockwise is negative. Student: I think I'm getting it. Angles are defined on the polar coordinate system the way they are on the unit circle, usually in radians. So, if you are given the polar coordinate (3, π/4), the point is three units from the center with an angle of π/4 radians measured counterclockwise from the polar axis:
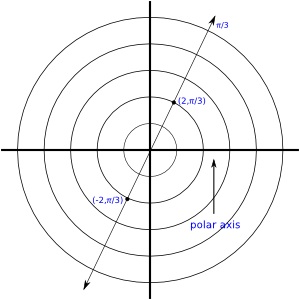
Student: So it sounds like coordinates given can be negative too? Mentor: That is an excellent question and the answer is yes. Just as on the unit circle, negative angles go in a clockwise direction from the polar axis. Do you remember -3π/4 is the same as 5π/4? Student: Yes and -4π/3 is the same as 2π/3? Mentor: That's right. And, since you can add as many rotations in the form of multiples of 2Ï as you want, any angle can have an infinite amount of negative and positive values. In addition, r can be negative. A negative r indicates that the point is in the opposite quadrant from the angle given in the coordinate pair. For example π/4 is located in the 1st quadrant, so positive r values are plotted r units from the pole in the 1st quadrant and negative values are plotted in the opposite quadrant, the 3rd quadrant, on the angle identified as 5π/4. Where do you think the point (-2, π/3) is plotted? Student: Well, since (2, π/4) was measured 2 units to the right along the polar axis, then -2 would indicate that the point is measured 2 units to the left along the polar axis and then π/4 degrees in the counterclockwise direction. Since the angle π/3 is in the first quadrant, then to plot the point (-2, π/3) you would plot a point two units from the pole along the angle 4π/3. Right? Mentor: That's right. It would look like this:
Student: So a single point could have many different values? Mentor: Correct! The values for r can be given as positive and negative values and θ can be given not only in positive and negative values, but also as any value θ + any multiple of 2π. So, unlike the Cartesian system where each point has a unique set of coordinates, in the polar system any point can have an infinite number of coordinates! Student: That means that the point given as (2,π/4) could also be given as (2,-7π/4) or (2, 9π/4) or (-2,5π/4)! Mentor: Exactly. Try plotting those points using the Polar Coordinates activity and verify they are the same point! |