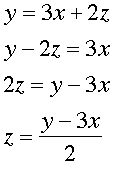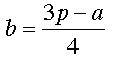Independent and Dependent Variables
|
Mentor: Today we are going to discuss independent and dependent variables. What does it mean for something to be independent? Student: That means that it doesn't depend on anything else. Mentor: That's right! So what do you think it means for a variable to be independent? Student: Maybe that variable doesn't depend on the other variables or numbers. Mentor: Correct. In mathematical terms, we call a variable independent if its value can be set arbitrarily to get a result. This is known as the input of a function. Do you know what I mean by "input"? Student: That's the variable that you start with. You know that variable, then you do something to it, and you get the "output". Mentor: Right, and we represent the variables with x and y. When you input a value of x into an equation, you get a value for y. So if x is the independent variable, what identity does y have? Student: Since y is the output of the function, I guess y would be the dependent variable. Its value is dependent on whatever the value of x is. Mentor: That's right, y is the dependent variable because we do not set a value of y directly; instead, we set a value of x and use that to find the value of y. Consider this simple equation as an example:
Mentor: In this equation, what are the independent and dependent variables? Student: Well, for any value of x, you have to multiply it by two and then add one to get y, so y is dependent on x. The independent variable is x, and the dependent variable is y. Mentor: Indeed. It is relatively easy to identify the independent and dependent variables in a simple two-variable equation, but what do you make of this equation:
Student: Yikes! I don't know what to do with more than two variables. I guess y would still be the dependent variable, but I don't know which of x and z is the independent variable. Mentor: You're right on both counts. x and z are both independent variables. You can change either variable to any value before determining the value of y. Student: Okay, I think I've got it. The variable that's alone is the dependent variable, all other variables are independent. Mentor: That's right, but what if I change the equation around a bit? What happens when I solve the equation for z:
Student: Then... z is the dependent variable, and x and y are independent. But I thought you said that y was the dependent variable. Mentor: I did say that, but the independent and dependent variables are not so immutable as they might seem from an algebraic perspective. With any equation, you can arbitrarily set any variable as the dependent variable, and then set all others as independent variables. In fact, what you've learned about dependent and independent variables has very little to do with pure algebra. Student: Then why bother? Why not just randomly pick out variables to be independent and dependent? Mentor: Consider the idea of driving a car. The acceleration of the car changes based on the pressure you put on the accelerator and the brake, approximated by the equation:
Mentor: Where a is the acceleration, p is the pressure on the accelerator, and b is the pressure on the brake. In this equation, what is the dependent variable? Student: Acceleration, a is dependent. Mentor: Right, but even if I rearranged the equation to read:
Mentor: It wouldn't make any sense to say that the pressure you put on the brake depends on your acceleration. Clearly, it is acceleration that depends on braking, not the other way around. And pressure on the brake certainly doesn't depend on pressure on the accelerator. Student: So I guess when you are talking about real-world phenomena, the idea of independent and dependent variables becomes more important. Mentor: Exactly. Especially when you start learning to perform scientific experiments, the idea of independent and dependent variables will be important conceptually, even if it is not important algebraically. |