Functions and the Vertical Line Test
|
Student: I am having some trouble deciding whether some of the more complex graphs are functions or not. Mentor: There are many ways to tell if it is a function. Student: Are there any that can be done by just looking at the graph? Mentor: As a matter of fact there is. It is called the vertical line test. Student: What does a vertical line have to do with functions? Mentor: Look at one of the graphs you have a question about. Then take a vertical line and place it on the graph. If the graph is a function, then no matter where on the graph you place the vertical line, the graph should only cross the vertical line once. Student: Really? Does that work all of the time? Mentor: Yes, all of the time. Let's try one.
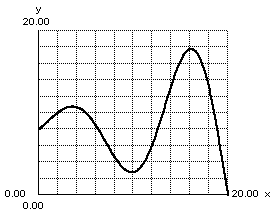
Can you tell me if that is a function in that plot? Student: Yes, that is. I can't put a vertical line anywhere on this graph and have it touch the function more than once. This works great, especially if I can see the grid. Mentor: What about common shapes like circles and squares? Student: They are not functions. Mentor: Can you tell me why? Student: They would not pass the vertical line test. Mentor: Why don't they pass? Student: Both of those shapes pass through the vertical line twice in lots of places! Look, here's just one example:
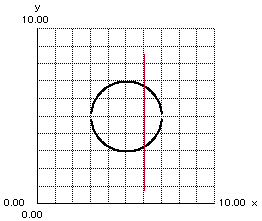
Mentor: Yes! Remember that hitting the vertical line more than once would mean that there are more than one y values for certain x values. This works for formulas when you are not sure whether they are functions. Any time you get more than one y value when you fill in an x value, it means that the formula is not a function. Having at most one y value for every x value means that there is a well-defined relationship, or in other words, a function. Student: That means that graphs such as x = 2 are not functions but graphs such as y = 2 are. Mentor: You are correct. Now lets try a harder one.
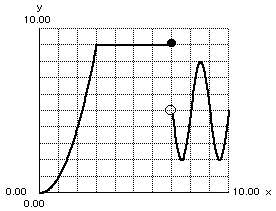
Student: What is going on at x=7? It looks like the graph jumps down? Mentor: That's right. It is up on the flat part at x=7, but for x larger than 7 it is on the curvy part. That colored in dot tells us that at 7 we should use the y-value 9, the dot with no shading tells us that the curvy part of the graph is what to use for anything larger than x = 7, but not for 7 itself. We call this a piecewise graph, and when we have this situation, we need to be told where the open and closed (filled or not) circles are. Student: If that is how you read it, then this is a function. Nowhere on this graph can I make a vertical line touch the function in more than one place. This makes things a lot easier and it makes sense. Mentor: Can you draw me a graph that is not a function? Student: Sure! Here's one:
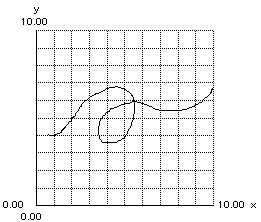
What are these called? Mentor: Well, every graph that describes a relationship between x and y is called a relation. Also, graphs that are drawn on the cartesian plane are called plane curves, 2-dimensional curves, or simply curves. So, functions are all of these things, but to answer your question, graphs that are not functions can be called by any of these names. |
