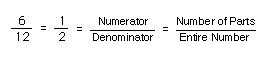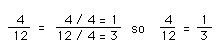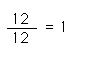Fractions
|
Student 1: I thought we were studying fractions now, so what do fractions have to do with a carton of eggs? Mentor: Suppose we were mixing up a batch of blueberry muffins and the recipe called for four eggs. How would we represent four of the eggs in the carton as a fraction? Student 2: Well, twelve eggs come in a carton, so the fraction would be 4/12, or four parts out of twelve. Mentor: Good. And if we look in the carton after we take out the eggs, we see an example of what four out of twelve looks like. Mentor: And if we remove two more eggs, we see what six out of twelve, or 6/12 eggs looks like.
Student 1: Yes, six out of twelve is exactly half of the eggs. Mentor: That's right. We can reduce the fraction 6/12 to one half, or 1/2. These two fractions are the same. Student 1: Can we reduce the fraction 4/12? Mentor: In the same way that six is half of twelve, or 1/2, four is one third of twelve, or 1/3. Both numbers can be divided by four: 4 divided by 4 is 1; 12 divided by 4 is 3, so the fraction is 1/3.
Student 2: What fraction is it if we remove all the eggs? Student 1: There would be no eggs left, 0/12, or zero, so there wouldn't be a fraction, because there cannot be a part of nothing, right? Mentor: Good thinking. Nothing is always nothing, so we can't remove some of it, or divide it into parts. Student 2: Then what if we didn't take out any parts at all; what if we left all the eggs in the carton? Student 1: The fraction would be 12/12, which would be the same as ... Mentor: One. Twelve out of twelve eggs equals one entire carton of eggs. Any fraction that has the same numerator and denominator equals the number 1.
Student 2: OK, I understand that now. I'm ready to make blueberry muffins! |