Cross Sections
|
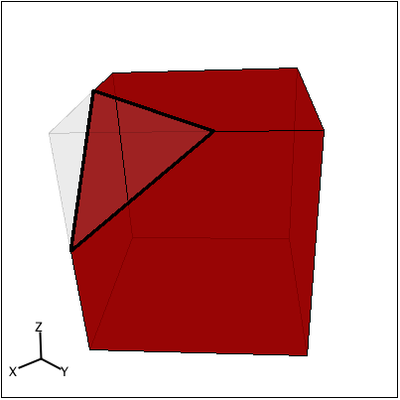
Mentor: If you cut a slice of a cube, what shape cut is created? Student: A square! Mentor: Is that always true? What if you cut the cube at an angle? Student: Well, then two of the sides would be longer than the other two, so I guess the shape would be a rectangle. Mentor: That's right. Now what would happen if you cut the cube at a different angle - say, if you just cut off the very tip of the cube? Student: Then...I guess it would be a triangle, like this:
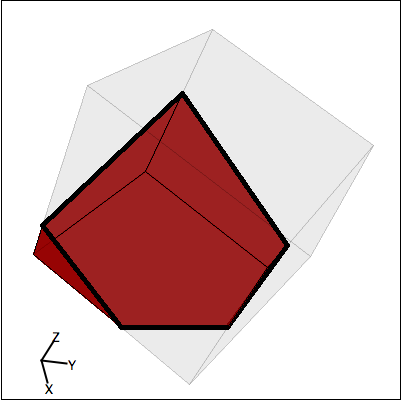
Mentor: Exactly! What other shapes do you think could be created by cutting a cross section of a square? Student: Hmm, well I bet that if you can create a triangle by cutting off just a corner of the cube, then you can create a pentagon by cutting off a bigger chunk, like this:
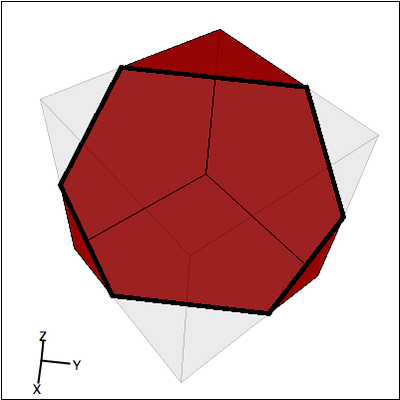
Mentor: That's good, so you see that you can create a cross section with more sides than the original shape. What would happen if you angled the cross section even more, so that the top corner of the cross section was cut off as well? Student: Then you would have...a hexagon!
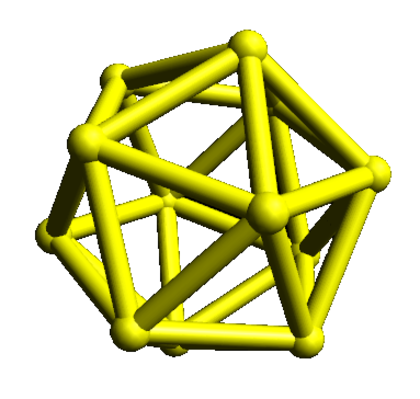
Mentor: Exactly! Do you think you can contruct a figure with more sides, such as a heptagon? Student: I can't figure out how to do that, since I can't seem to cut off more than two of the four corners. Mentor: Don't worry, what I asked you to do is actually impossible! There are only six faces on a cube, so the highest number of sides possible is six. Student: That makes sense. I bet you can do that with any prism - it's just a matter of angling the cross section correctly to intersect all of the faces. Mentor: You're very right, any prism can be cut in such a way that the cross section has as many sides as the prism has faces. However, not all shapes have this same property. Can you think of a 3-dimensional figure whose sides cannot all be sliced through by the same plane? Student: Perhaps an Icosahedron, because there is no plane that can intersect all twenty of its sides:
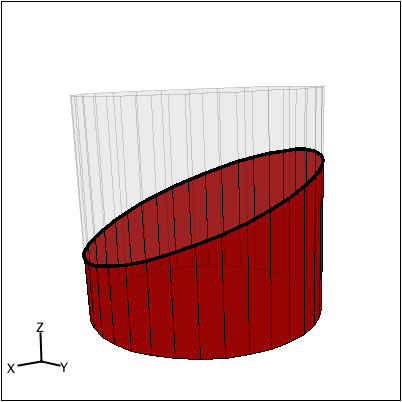
Mentor: Good, the Icosahedron is an example of a polyhedron that is not a prism. If we consider prisms only, what would happen to the cross sections of a prism if the number of lateral faces approached infinity? Student: I've never heard of an infinity-sided prism... Mentor: Well, when you are trying to visualize something you haven't seen before, try building off of what you already know. Imagine a regular square, then a regular pentagon, then a regular hexagon, and so on. As the number of sides gets larger, what other shape does the figure approach? Student: Hmm, it's starting to look more like a circle because you can't see any of the individual sides. Mentor: Exactly. In fact, mathematicians formally define a circle as a regular polygon with an infinite number of sides. So what would happen if you sliced into a circular prism, also known as a cylinder? Student: Well, obviously you could make a circle if you cut the figure horizontally, and you could make a rectangle if you cut the figure vertically. More interesting, though, is the fact that you can make an oval if you cut a cylinder through at an angle:
Mentor: There are an infinite number of three-dimensional shapes, each one with its own cross section. In fact, every two-dimensional shape can be defined as a cross section of a three-dimensional shape. This will come in handy when you discuss Conic Sections, but it will also be useful if you decide to take Multivariable Calculus and other high-level math classes. Student: Why define two-dimensional shapes as cross sections? Why not just leave them in two dimensions? Mentor: When dealing with two-dimensional shapes, usually it is simpler to just leave them in two dimensions. A big use of cross sections, though, is to calculate the volume of irregular figures. When you take Calculus, you will learn how to calculate the area of almost any two-dimensional shape. Since a three-dimensional object can be divided into a large number of cross-sections, the areas of those cross-sections can be used to calculate the volume of the three-dimensional object. |