Continuous Distributions: Infinite Trials, Infinite Possibilities
|
Student: When I was looking at the normal distribution and the skewed distribution activities, I noticed that the histograms never looked much like the curves. When I made the bin size very big, the heights looked good but it looked like a row of large blocks. When I made the bin size small, the heights were very blocky because they only had a few values. Mentor: Very good. Student: So what do the curves really mean? Are they just guesses? Mentor: In a way it is as if you took an average of all the graphs you made, with all the different bin sizes. But there is a better mathematical way to look at it. Do you remember experimental and theoretical probability? Student: Yes. Theoretical probability is when you add up the favorable outcomes and divide them by the total outcomes. Experimental probability is when you try an experiment a lot of times, and divide the successes by the trials. Mentor: And when you did something a lot of times, those two numbers got very close to each other, didn't they? Student: Yes. Mentor: And if you did it an infinite number of times, which is to say if you did it forever, you'd actually get back the theoretical probability. You'll learn more about infinity when you study fractals, but for now what's important about it is that big numbers that are not infinite act more and more like infinity as they get closer to it. So we can believe that the theoretical probability of something is the same as if you ran the experiment an infinite number of times. Student: So if I flipped a coin, and kept track of the number of heads, forever, I'd really get half heads. Mentor: Yes. And if you flipped two coins at a time, and kept track of how many heads you got each time, you might get a histogram like this:

Student: That looks like some of the histograms I had when I set the bin size very large. Mentor: Yes. It wouldn't make sense to change the bin size on that graph, but what if we flipped more than two coins? Then there would be more possible values. If we flipped twenty coins each time, the theoretical graph looks like this:
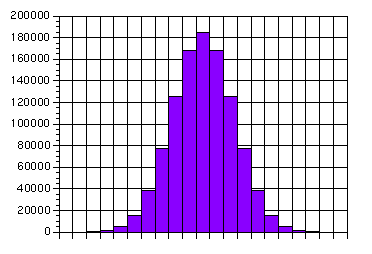
Student: That looks more like the normal curve than a lot of my histograms. Mentor: Remember this is infinite trials. But you are seeing something that is important. As you have more and more coins per flip, you have more and more possibilities. When you have infinite trials, you get back an exact theoretical height, and as you get out toward infinite possibilities, you get more and more points with intermediate heights. When you have infinite possibilities and infinite trials, you get a smooth curve. Now how do you think this might be different between statistics and probability? Student: Well, in statistics you can't always repeat the same experiment twice, much less infinite times. Mentor: There's one more thing. In statistics you have as close to infinite possibilities as your measurement allows, partly because of what you just said. You might be measuring the heights of different plants, which could have an infinite number of random variables controlling how tall they grew. But the same idea still works. If you perform an infinite number of trials of an experiment with infinite possibilities, then the result will be a smooth theoretical curve. Student: And that's what the normal curve is! |
