Conic Sections
|
Mentor: Today, we're going to talk about conic sections. Do you know what the four conic sections are? Student: They're the Parabola, Hyperbola, Ellipse, and Circle, right?
Mentor: That's right. If you look at the graphs of each of these conic sections, you'll see that they
look very different.
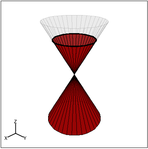
Student: Do they have something to do with cones? Mentor: Absolutely! All of the graphs can be formed by the same process. First of all, what is a cross section? Student: That's when you slice a three-dimensional object with a plane, creating a two-dimensional object. Mentor: Exactly! So conic sections are just cross sections of a double cone. What do I mean by a "double cone"? Student: That's two cones, right? Where the points of the cones are just barely touching. Mentor: That's right! Why might I need two cones to make conic sections? What about these cross sections requires two cones? Student: The hyperbola has two sides, so you need two cones to create it. Mentor: That's right! The way you cut the cones can create each of the different conic sections. Can you find the ways to create each one?
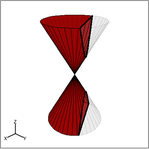
Student: The circle is made by slicing the double cone exactly parallel to its base, like this:
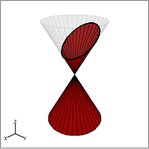
Mentor: That's exactly right. Now let's think about the ellipse. It's sort of a mix between a parabola and a circle, right? So how do you slice the double cone?
Student: The ellipse is any slice between a parabola and a circle, right? Like this:
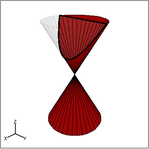
Mentor: Exactly! Now what about the hyperbola? Student: I don't know, because a parabola that intersects both cones is a hyperbola. Shouldn't it just be the same as a parabola? Mentor: But you said that a parabola is something parallel to the edge of the cone. What do we know about the definition of parallelism? Student: When two lines are parallel, they never intersect. So if a parabola is created by a slice that is parallel to the edge of the cone, it can't be a hyperbola. Is a hyperbola created by slicing the double cone at any point between the two parabola planes?
Mentor: That's right! Just like in this picture:
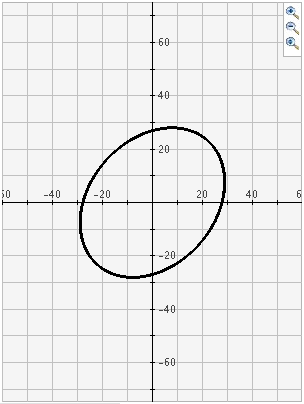
Student: Oh, I get it! Mentor: So that's the geometric definition of the different conic sections, but how would you be able to define each of these figures algebraically? Student: Well, for a circle I know that you just need the center and the radius to define it uniquely. Mentor: Precisely! As it turns out, you can find some version of the "center" and "radius" for all of the conic sections. For instance, the elipse is just a circle that has been stretched or compressed in one direction, so all you need to find the location of an ellipse is the center, the radius of the major axis, and the radius of the minor axis. Student: So the major and minor axes are like the radius of the circle horizontally and vertically? Mentor: Usually, but remember that an ellipse could be stretched diagonally or some other direction that isn't exactly horizontal or vertical, like in this figure:
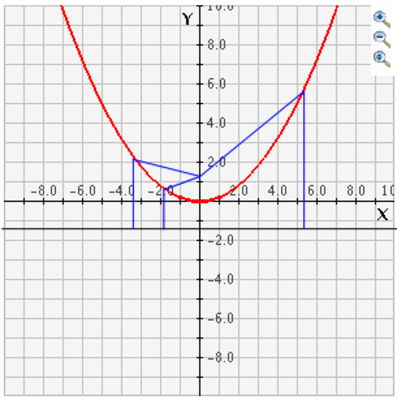
Student: Oh, that's right. That figure would have a major axis along the line y = x and a minor axis along the line y = - x. Mentor: Correct! Now, what information do you need to know about a parabola? Student: Hmm, there is no real center to a parabola, but I think that if we knew the vertex and how steep the curve was, we could define the curve. Mentor: We do indeed need to know the vertex, but instead of finding how steep the curve is, we can use another special property of parabolas. What do you notice about the pairs of blue lines in this graph?
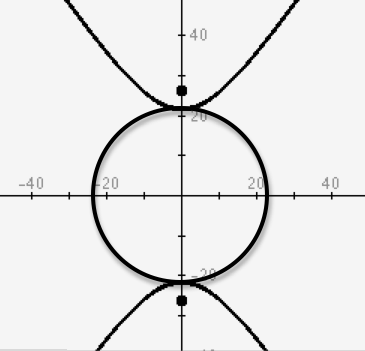
Student: In each pair of lines, the line from the focus to the curve looks about the same length as the line from the curve to the black line below. Mentor: Exactly! In fact, that is the definition of a parabola: the set of all points equidistant from a focus and another line, which is called a directrix. Student: That makes sense. A parabola is defined basically the same way as a circle. Mentor: Now, what can we do with a hyperbola? How can we define two back-to-back curves? Student: Perhaps we could find a center between the two curves, and then measure the distance between them. Mentor: That's certainly a part of it, but actually, for every hyperbola there is an associated circle or ellipse:
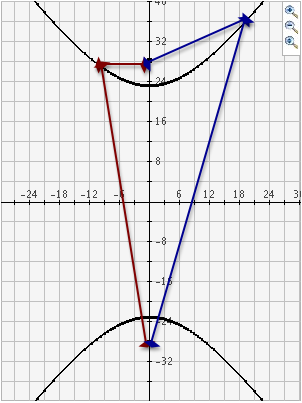
Mentor: All we really need to know is the center, major axis, and minor axis of the ellipse (or the center and radius of the circle) to be able to define a hyperbola. Student: But how can we find the axes of an ellipse that isn't drawn? Mentor: Similar to the way all points are equidistant from the focus of a parabola, for a hyperbola you can find the distance between a point on the parabola and each of its foci:
Mentor: Whereas in a parabola the two distances are equal, tn the case of a Hyperbola, the difference between those two distances is always constant. |

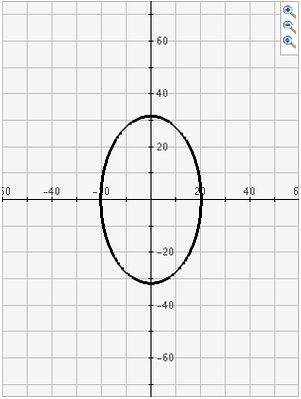
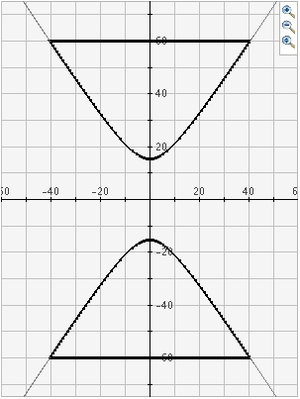
 What do you suppose makes them conic sections then?
What do you suppose makes them conic sections then?
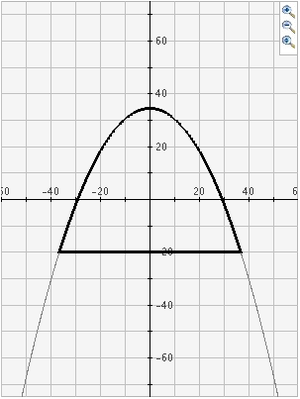
 And the parabola is made by slicing the double cone exactly parallel to the edge of the double
cone, like this:
And the parabola is made by slicing the double cone exactly parallel to the edge of the double
cone, like this: