Angles
|
Mentor: Today we are going to learn about angles. Student: I know what an angle is! It is two rays connected together. Mentor: Good job! Did you read that from your book? Student: Yes. Mentor: Well, there are three categories of angles: acute, obtuse and right. Let's learn what a right angle is first. Right angles are present many places in real life. Look at the corners of this room or the edges of your books. A right angle is an angle that measures 90 degrees. A right angle looks like this:

Mentor: The second type of angle is acute. An acute angle is an angle whose measure is between 0 and 90 degrees. An acute angle looks like this:

Student: Let me guess! The third type is an angle whose measure is more than 90 degrees. Mentor: Yes, an obtuse angle is an angle whose measure is between 90 and 180 degrees. An obtuse angle looks like this:

Mentor: We also have names for pairs of angles. Angles are formed when lines intersect. We are going to look at the angles formed when two parallel lines are intersected by a third line called a transversal . In this picture, the red lines are parallel and the blue line is the transversal.
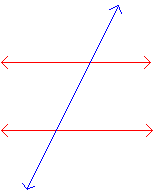
Student: Those lines formed 8 angles. Mentor: Good job. Now, who can show me an acute angle? Student: I can! It is the one on the top right.
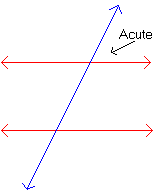
Mentor: Right again. Who can show me an obtuse angle? Student 2: I think it is the one on the top left.
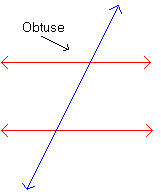
Mentor: Correct. We need an easier way of referring to the angles we are talking about. So from now on, we will label our angles. Angles a and b are adjacent angles.
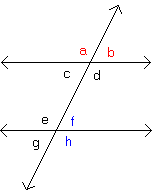
Mentor: Angles f and h are also adjacent angles. Does anyone know what it means for a pair of angles to be adjacent? Student: Does it mean that they are side by side? Mentor: Yes, adjacent angles are angles that share a ray. Can anyone tell me another pair of angles that are adjacent? Student: Yes, angles c and d are adjacent. Student 2: I can too; angles b and d are adjacent. Mentor: Good job, angles c and d are adjacent and so are angles b and d. There are many pairs of adjacent angles in the picture. Now, let's talk about vertical angles. Angles a and d are vertical angles.
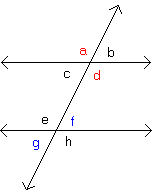
Mentor: Angles f and g are also vertical angles. Can anyone guess what it means for a pair of angles to be vertical? Student: Are vertical angles ones that are opposite from each other? Mentor: Good job! Vertical angles share only one point. That point is called the vertex. Can anyone name another pair of vertical angles? Student 2: I can; angles b and c are vertical angles. Student: Angles e and h are also vertical angles. Mentor: Yes, angles b and c are vertical angles and so are angles e and h. Now that we know what adjacent and vertical angles are, let's talk about alternate interior angles. Angles c and f are alternate interior angles.
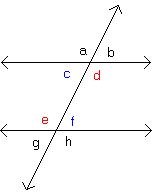
Mentor: Angles d and e are also alternate interior angles. Who knows what it means for two angles to be alternate interior angles? Student: Are alternate interior angles the ones that are inside the lines and on opposite sides from each other? Mentor: Yes, alternate interior angles are angles that are inside the parallel lines and on opposite sides of the transversal. Now, who thinks they can guess what alternate exterior angles are? Student: They are the angles on the outsides of the parallel lines and on opposite sides of the transversal. Mentor: Correct again. Who can give me an example? Student: Angles a and h are alternate exterior angles.
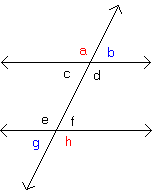
Student 2: Angles b and g are also alternate exterior angles. Mentor: Great job. It's time for the angles game . |
